Multifractal analysis

A direct use of the local regularity is often fruitful in applications. This is for instance the case in the analysis of ECG, or terrain modelling. However, in some situations, it is interesting to supplement or replace it by a more global approach known as multifractal analysis (MA). The idea behind MA is to group together all points with same regularity (as measured by the pointwise Hölder exponent α(t)) and to measure the “size” of the sets thus obtained. There are mainly two ways to do so, a geometrical and a statistical one.

In the geometrical approach, one defines the Hausdorff multifractal spectrum of a process or function X as the function:
                              α→ fh(α) = dim{t : α(t) = α},
where dim(E) denotes the Hausdorff dimension of the set E.
This gives a fine measure-theoretic information, but is often difficult  to compute theoretically, and almost impossible to estimate on numerical data.
The statistical path to MA is based on the so-called large deviation multifractal spectrum:

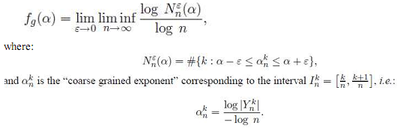
Here, Yn,k is some quantity that measures the variation of X in the interval In,k, such as the increment, the oscillation or a wavelet coefficient.
The large deviation spectrum is typically easier to compute and to estimate than the Hausdorff one. In addition, it often gives more relevant information in applications.

Multifractal spectra subsume a lot of information about the distribution of the regularity, that has proved useful in various situations. A most notable example is the strong correlation reported recently in several works between the narrowing of the multifractal spectrum of ECG and certain pathologies of the heart. Let us also mention the multifractality of TCP traffic, that has been both observed experimentally [ref] and proved on simplified models of TCP [ref].
MA is a very active field of research worldwide. Our current work focuses on the following points:

1. compute the multifractal spectra of self-regulating processes,
2. compute the multifractal spectra of some classes of multistable processes, in particular multistable Lévy motions and linear multifractional multistable motions,
3. compute the multifractal spectra of PDP or (renormalized) sums of PDP. We use PDP to model the concentration of drugs in the case of non-compliance in our pharmacodynamics application.