Multistable Processes

Non-continuous phenomena are commonly encountered in real-world applications, e.g. financial records or EEG traces. For such processes, the information brought by Hölder exponents must be supplemented by a  measure of the density and size of jumps in order to get a better description of local regularity.

Stochastic processes with jumps, and in particular Lévy processes, are an active area of research. The simplest class of non-continuous Lévy processes is maybe the one of stable processes. These are mainly characterized by a parameter α ∈ (0, 2], the stability index (α = 2 corresponds to the Gaussian case, that we do not consider here). This index measures in some precise sense the intensity of jumps. Paths of stable processes with α close to 2 tend to display “small jumps”, while, when α is near 0, their aspect is governed by large ones.

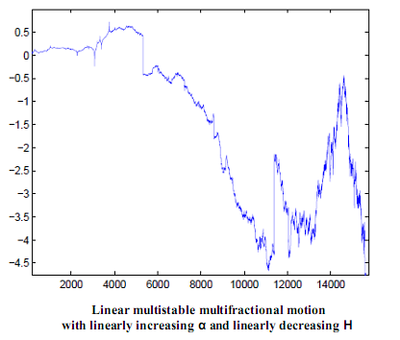
In line with our quest for the characterization and modelling of various notions of local regularity, we have defined multistable processes. These are processes which are “locally” stable, but where the stability index α is now a function of time. This allows to model phenomena which, at times, are “almost continuous”, and at others display large discontinuities. Such a behaviour is for instance obvious on almost any sufficiently long financial record.

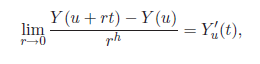
where the limit is taken either in finite dimensional distributions or in the sense of distributions.

 Our approach for defining multistable processes is similar to the one developed for constructing mBm: we consider fields of stochastic processes X(t, u), where t is time and u is an independent parameter that controls the variation of α. We then consider a “diagonal” process Y (t) = X(t, t), which will be, under certain conditions, “tangent” at each point t to the process t → X(t, u).

A particular class of multistable processes, termed “linear multistable multifractional motions” (lmmm) takes the following form.

Let (E, E, m) be a σ-finite measure space, and ∏ be a Poisson process on E × R with mean measure m × L (the Lebesgue measure). An lmmm is defined as:

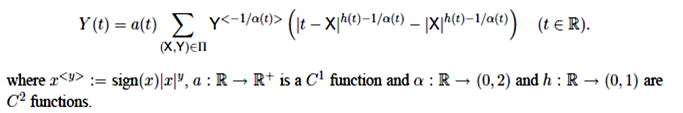
The couple (h, α) allows to prescribe at each point, under certain conditions, both the pointwise Hölder exponent and the local intensity of jumps. In this sense, lmmm generalize both the mBm and the linear multifractional stable motion. From a broader perspective, such multistable multifractional processes are expected to provide relevant models for TCP traces, financial logs, EEG and phenomena displaying time-varying regularity both in terms of Hölder exponents and discontinuity structure.

Another approach for defining multistable processes is using characteristic functions to construct -multistable measures and integrals, where the measures behave locally like -stable measures, but with the stability index  varying with time .

Let
 
 we define the space of the functions

The multistable stochastic integral of a function  can be specified by the finite-dimensional distributions of as a stochastic process on the space of functions .

Formally speaking, let and where for all . Then 

 for , is the characteristic function of a probability distribution on the random vector 

. Let be the sets of finite Lebesgue measure. We

define the -multistable random measure by

for , where is the indicator function of the set .

Different from the other definition, the multistable processes defined by finite-dimensional distributions have independently scattered property.

One of the simplest case of multistable processes is multistable Lévy motion. It can be defined by

And

where and .

There are two other equivalent definitions of multistable Lévy motion:

i) The multistable Lévy motion defined by Poisson representation is

where is a Poisson process, , sign and

ii) The multistable Lévy motion defined by series representation is

where

is a sequence of arrival times of a Poisson process with unit arrival time, is a sequence of i.i.d random variables with uniform distribution on , and is a sequence of i.i.d random variables with distribution , and all three sequences , and are independent.


We are currently investigating the following points in relation with multistable processes:

1.  the multifractal properties of stable processes are well known. Indeed, the multifractal spectra are deterministic, with a shape governed by the index α. It is of interest to characterize the multifractal properties of multistable processes. This seems difficult to perform in full generality, and we concentrate as a first step on the case of lmmm and other particular processes.
2. Self-regulating processes are defined as processes where the local regularity is a deterministic function of the amplitude. It seems natural to follow the same approach and define “self-stabilizing processes” as processes where the local index of stability is a function of the amplitude.
3. Higher dimensional extensions would be useful, for instance for the modelling of medical images or natural terrains.
4. For applications, robust statistical estimation of α(t) (or of the couple (α(t), h(t)) in the case of lmmm) is necessary. We are studying estimators in that view.