Self Regulating Processes

We have recently introduced another stochastic model, inspired by mBm, but where the local regularity, instead of being tuned “exogenously”, is a function of the amplitude. In other words, at each point t, the Hölder exponent h(t) of the process X verifies almost surely h(t) = g(X(t)), where g is a fixed deterministic function verifying certain conditions. A process satisfying such an equation is generically termed a self-regulating process (SRP). The particular process obtained by modifying adequately mBm is called self-regulating multifractional process (SRMP), but there are other ways to obtain the self-regulating property. The motivation for introducing self-regulating processes is based on the following general fact: in nature, the local regularity of a phenomenon is often related to its amplitude. An intuitive example is provided by natural terrains: in young mountains, regions at higher altitudes are typically more irregular than regions at lower altitudes. We have verified this fact experimentally on various terrains. Other natural phenomena displaying a relation between amplitude and exponent include temperatures records and RR intervals extracted from ECG.

To build SRMP, one starts from a field of fractional Brownian motions B(t,H), where (t,H) span [0, 1] × [a, b] and 0 < a < b < 1. For each fixed H, B(t,H) is a fractional Brownian motion with exponent H. Denote:

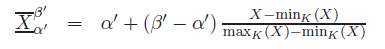
the affine rescaling between α′ and β′ of an arbitrary continuous random field over a compact set K. One considers the following (stochastic) operator, defined almost surely:

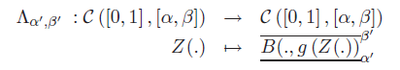
where α ≤ α′ < β′ ≤ β, α and β are two real numbers, and α′, β′ are random variables chosen adequately. One may show that this operator is contractive with respect to the sup-norm. Its unique fixed point Z* is SRMP. Additional arguments allow to prove that, indeed, the Hölder exponent h at each point of Z* is almost surely equal to g(Z*(t)).

Click below for a short animation showing a self-regulating multifractional process with prescribed shape.

 Left: strength of the prescribed shaping. Right: prescribed shape (cyan), self-regulating process with g=Id, i.e. h=Z (blue) and estimated exponent (red). Animation O. Barrière.

We believe that SRP open a new and very promising area of research. We particularly focus on the following:

1. One may think of other ways of obtaining the self-regulating property. In addition to building SRP by modifying Lévy’s construction of Brownian motion, or using wavelets, SDE approaches would be interesting.
   
2. Another obvious extension is to construct processes such that α(t) =g(X,Y), where Y is a process dependent or not on X. For instance, Y could be a primitive of X, leading to "integro-differential self-regulating equations”. Or, in the context of ECG, Y could subsume information on external factors impacting RR intervals.
3. The probabilistic properties of SRP, apart from regularity, have yet to be studied. They will probably require delicate tools, as the definition of an SRP, is, in most cases, implicit. In addition, these processes can never be Gaussian, since their Hölder exponent is random.
4. In applications, it is crucial to be able to estimate the function g which characterizes an SRP. This does not seem to be an obvious task, as the tools developed for estimation in the case of, e.g., fBm or mBm do not apply. In the case of SRMP, the determination of the local time of the process seems to be a necessary step for proper estimation of g.
5. An interesting fact is that the study of the multifractal properties of an SRP also seems to involve its local time. The multifractal spectra of SRP should have interesting properties, as they will be random quantities governed by the deterministic function g.